Page 25 – Algebra Comes to the Rescue
The power curves take
a lot of time to create.
The
chart on the previous page had 12 sets
of power level readings.
At
three or more readings per power level, at one minute intervals,
that can be 40 minutes.
If we use some algebra, this
time can be reduced dramatically.
When we ask the
computer to fit a curve to the data points it comes up with
an
equation of the type ………y=
ax2
+ bx + c
A
“hilltop” chart. As we saw on pages 21 and 23.
Now,
back in my days at school, we were taught differentiation.
So differentiating
the equation above. .....dy/dx
= 2ax + b
And
this represents the gradient of the power curve for any value of
x,
the engine speed.
But at the peak of the curve, the
gradient is zero, so 2ax
+ b = 0 for the peak
power point.
Or x = peak power engine speed =
– b / 2a
Wouldn’t
it be good if we can find values for a
and b.
We
can – they specify the
downward slope of the torque chart. (a
is negative)
So, if we plot torque vs engine speed
and ask the computer to do a
straight line fit,
it
will give us the values for a
and b,
See the chart opposite.
From the experimental
measurement viewpoint, getting data for a straight line
is
far easier than for a curve. Only two points are needed. So, for
experimental rigour,
how about we take readings for three
load points on the engine.
Three points in a straight line
prove that there is no curve.
Three measurements at
each load gives nine readings.
At one minute per reading, the
job is over in ten minutes!
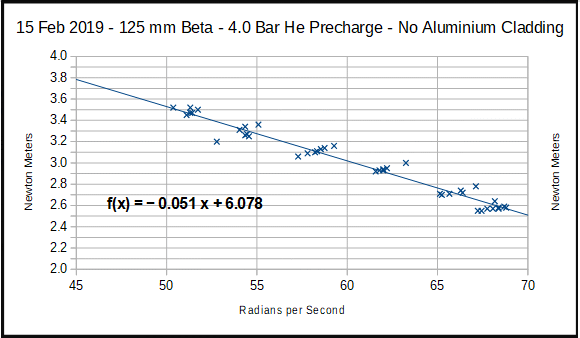
On the torque chart above, “Mr are we sure about this?”,
has run seven load settings.
The slope of the line is
downward, so a
is negative. a =
– 0.051
And
b
is the intercept on the y axis when x=0.
ie b= 6.078
Please
note that this chart is Newton meters vs Radians per
second.
(Multiply the radians by 10 to get an approx RPM
value)
This is the SI system (Le Système International) – no 360 degrees, no
minutes,
no ft-lbs.
Instead
- Radians, seconds and Newtons. Let’s
use “this century” science.
From
above, we
said the peak power speed is at –
b / 2a = – 6.078 / (2 x – 0.051)
The minus signs cancel and 6.078
/ 0.102 = 59.58
Rads/sec
And with 9.549 radians to 360 degrees, peak
speed is at 569 RPM.